在众多的加热方式中，电加热以其高效、便捷和可控性强等优点，在工业、科研以及日常生活中得到了广泛的应用。而理解电加热过程中的温升变化，对于优化加热效果、确保设备安全以及节约能源都具有重要意义。这就离不开电加热温升计算公式，通过它我们能够准确地预测和分析温度的上升情况。

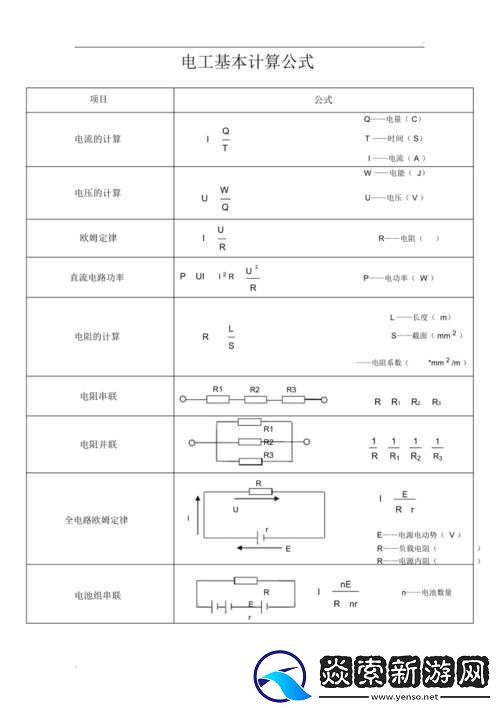
电加热温升的计算公式通常基于热力学原理和能量守恒定律。简单的电加热温升计算公式可以表示为：ΔT = Q / (mc) ，其中ΔT 表示温度的变化量，Q 表示所提供的热量，m 表示被加热物体的质量，c 表示物体的比热容。

比热容是物质的一个重要热物性参数，它反映了单位质量的物质温度升高 1 摄氏度所需要吸收的热量。不同的物质具有不同的比热容，例如水的比热容较大，而金属的比热容相对较小。这意味着相同的热量输入，水的温度上升相对较慢，而金属则升温较快。

在实际应用中，电加热温升计算公式的运用场景十分广泛。比如在工业生产中，对于金属材料的热处理，需要精确控制加热过程中的温度上升速率和最终温度，以达到改善材料性能的目的。通过计算输入的电能以及材料的质量和比热容，可以准确地预测温度的变化，从而调整加热功率和时间，确保热处理的质量。

再来看一个有趣的例子，在家庭中使用的电热水壶。当我们想知道多长时间能把水烧开时，就可以运用这个公式。假设电热水壶的功率是 1500 瓦，水的质量是 1 千克，水的比热容约为 4200 焦耳/（千克·摄氏度），初始温度为 20 摄氏度，要烧到 100 摄氏度。首先计算所需热量 Q = mcΔT = 1×4200×(100 - 20) = 336000 焦耳。而 1500 瓦 = 1500 焦耳/秒，所以加热时间大约为 336000÷1500 = 224 秒，约 3.7 分钟。但实际上，由于热量的散失等因素，实际加热时间会略长一些。

在实际应用中，我们还需要考虑到许多其他因素对温升计算的影响。首先是热量的散失，在实际环境中，被加热物体往往会通过热辐射、热对流和热传导等方式向周围环境散失热量。这就意味着实际输入的热量并不能完全用于物体的温升，需要对计算结果进行修正。加热过程中的不均匀性也会影响温升的计算。例如，在使用电阻丝加热时，靠近电阻丝的部分温度会升高得更快，导致温度分布不均匀。

为了更准确地应用电加热温升计算公式，我们可以采取一些措施。一是尽量减少热量的散失，通过良好的保温措施来降低热损失。二是优化加热方式，使得热量分布更加均匀。通过实验测量和实际数据的积累，可以对计算结果进行修正和验证，提高计算的准确性。

深入分析电加热温升计算公式的应用，我们还能发现它在新能源领域的重要作用。例如，在电动汽车的电池加热管理中，精确控制电池的温度对于电池的性能和寿命至关重要。通过温升计算，可以合理设计加热系统，确保电池在低温环境下能够快速达到最佳工作温度，同时避免过度加热对电池造成损害。

在科研领域，电加热温升计算对于材料研究也具有重要意义。研究人员可以通过控制加热条件和计算温升，来观察材料在不同温度下的结构和性能变化，为新材料的开发和应用提供理论依据。

电加热温升计算公式虽然看似简单，但在实际应用中却有着广泛而重要的作用。无论是工业生产中的工艺优化，还是日常生活中的小电器使用，甚至是前沿的科研探索，都离不开对它的准确理解和应用。通过深入研究和不断实践，我们能够更好地利用电加热技术，为各个领域的发展带来更多的便利和创新。随着科技的不断进步，相信这一计算公式也将不断完善和发展，为我们创造更加美好的未来。